Re: S00.眼鏡鏡片設計理論(序章)
※ 引述《jimmylin2002 (小吉米)》之銘言:
本文旨在分享鏡片設計的臨床應用實例及相關數理模型的分析,
期望能為讀者提供有價值的參考,推動視光學領域在理論與實踐方面的不斷進步。
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 111.71.87.119 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/optical/M.1755868453.A.CC2.html
→
08/25 08:41,
08/25 08:41
您好,誠摯感謝您撥冗閱讀。
這份回文想表達的,是我們對於知識與學問的一份初衷與信念。
我們所撰寫的文章與影片,不是複製轉述他人的結論,
也不是片段文字的拼湊,而是一場真切的數學探索。
全文皆以馬克思威爾方程式為唯一的起點與依歸
▽xE = -μ*δH/δt
▽xH = j +ε*δE/δt
▽。D = ρ
▽。B = 0
讓數學成為骨架,在推導的歷程中層層展現其內在的邏輯與秩序。
當今許多語言模型或科普式的解釋,看似能給出煞有其事的結論,
但往往僅止於語言表層的模仿,並不意味理解了數學方程的內涵。
---------------------------------------------------
我舉個例子,像是近期114年07月,榮吉教授閱覽教材時發現
https://i.meee.com.tw/Bc3X3JA.jpeg

視光教科書列載的消除球面像差的鏡片設計是有問題的。
https://i.meee.com.tw/cBSDSg9.jpeg
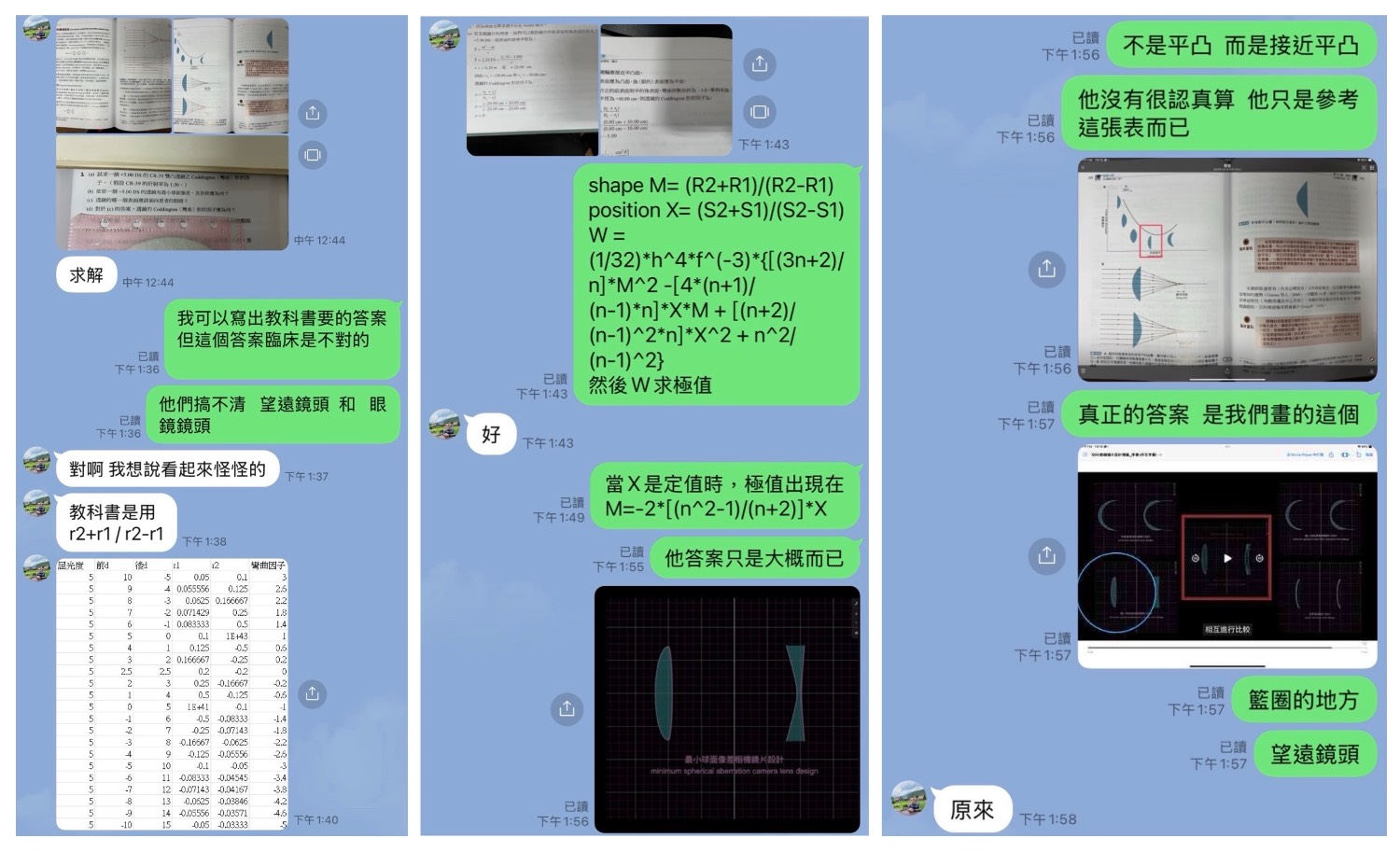
視光教材內文說明要消除眼鏡鏡片的球面像差
正透鏡需製作成前表面呈現凸面,後表面呈現接近平面;
負透鏡需製作成前表面呈現凹面,後表面呈現接近平面。
但實際上消除球面像差的眼鏡鏡片設計,
正透鏡應製作為前表面呈現凸面,後表面呈現凹面;
負透鏡應製作成前表面呈現凸面,後表面呈現凹面。
https://i.meee.com.tw/ZCmnQnI.jpeg

會出現這樣的誤植,
原因在於編撰教材的作者沒有真的理解方程式的內涵。
Define
shape factor M = (R2+R1)/(R2-R1)
position factor X = (S'+S)/(S'-S)
W(aberration) = (1/32)*h^4*f^(-3)*{[(3n+2)/n]*M^2
-[4*(n+1)/(n-1)*n]*X*M+[(n+2)/(n-1)^2*n]*X^2+n^2/(n-1)^2}
當X是定值時,W極值出現在 M = -2*[(n^2-1)/(n+2)]*X
當M是定值時,W極值出現在 X = -2*[(n+1)/(3*n+2)]*M
對於望遠鏡頭,
我們只需將物距為無窮遠,光闌設定為與鏡面重合,
此時最小球面像差鏡片形狀方程解為
[F/(F-2*F1)] = 2*[(n^2-1)/(n+2)]
上式可重新整理為
F1 = F*[n*(2n+1)/(2n+4)]
而這就是使用估狗搜尋,或著詢問Chatgpt所獲得的答案
但對於眼鏡鏡片,
我們需將像距變更為頂點距離,光闌設定與瞳孔重合,
最小球面像差成立的鏡片形狀方程此時將會變為另一形式
[F/(F-2*F1)] = 2*[(n^2-1)/(n+2)]*[F+2*(1/0.012)]
如果我們誤信教材內文,製作如上所示的消球差望遠鏡片,
佩戴者將會陳述影像異常模糊,物體劇烈形變,完全無法佩戴。
----------------------------------------------------
再舉個例,如市面上眼鏡鏡片廠商的行銷廣告詞宣稱,
“新一代漸進多焦設計,由於將累進帶從外表面改安置於內表面,
因為離瞳孔比較近,清晰視野範圍將會比舊有外表面設計寬廣。”
https://i.meee.com.tw/xUkwDex.jpeg
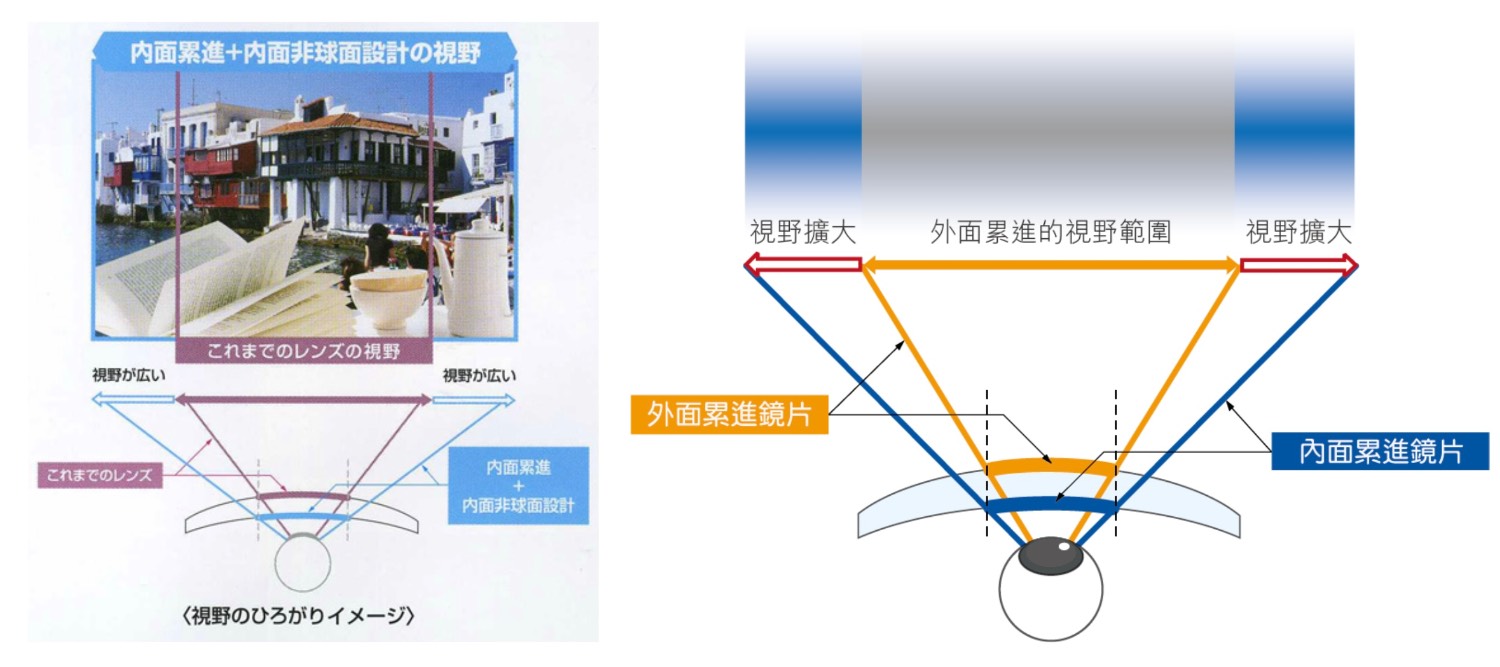
然而若驗光人員或消費者誤信廣告文宣,
為遠視患者選擇更昂貴的內面累進漸進多焦點設計,
他們將會經歷一場完全相反的糟糕驗配體驗,
近方清晰視野範圍將會異常狹小,跟宣傳文稿背道而馳。
如果我們有獨立思考與數學推演的能力,
便能以自身的理性判斷檢驗各種說詞與數據,
不致輕易受制於廠商所營造的片面敘事或誤導性宣傳,
而能在清晰的邏輯基礎上,做出真正符合事實真相的判斷。
----------------------------------------------------
影片與內文裡提及的特殊人名橢圓函數,
我們也沒有搜尋及閱覽到有相關深入探究的文獻。
然而我們深信推演出來的數學方程跟當時古人計算是一致的。
一位已故 Zeiss 視光工程師 Darryl J. Meister,
他生前曾經製作過一款眼鏡鏡片光學計算機,
https://opticampus.opti.vision/tools/downloads.php
計算機雖然沒有公開各項函數的完整數學表示式,
但其能直接輸出切爾寧橢圓與帕西瓦橢圓的圖像,
並能利用計算機算力直接列載無近似的精確數值。
我們利用馬克斯威爾方程遠焦近軸近似直接進行計算。
https://i.meee.com.tw/6sggUQj.jpeg

所推演出來的切爾寧圖樣跟計算機的輸出圖像是吻合的。
https://i.meee.com.tw/RcEd0qr.jpeg
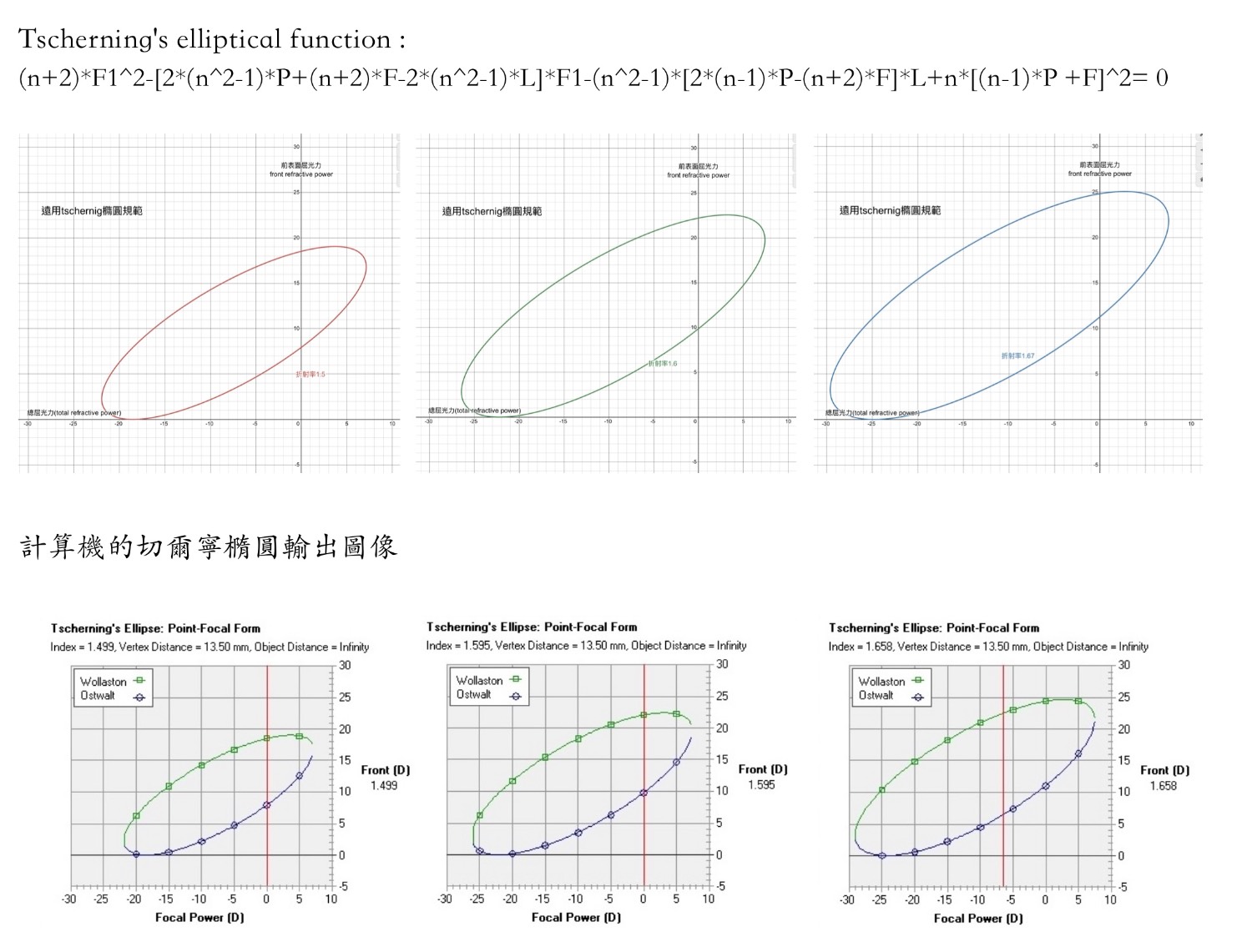
雖然我們的帕西瓦圖樣跟計算機的輸出圖像是不同的。
https://i.meee.com.tw/6srvyWF.jpeg
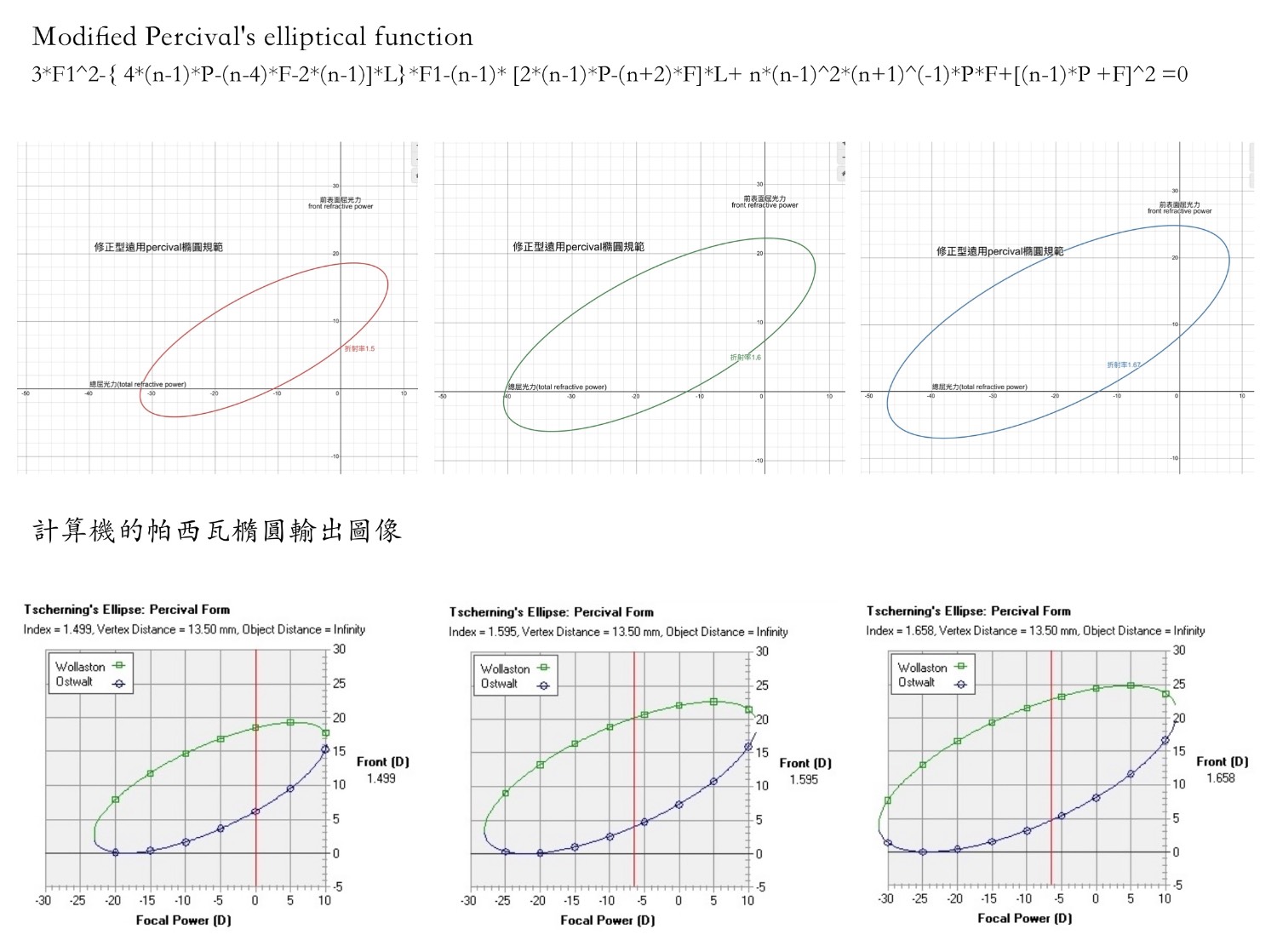
但是跟利用計算機算力無近似的列載數值是契合一致的。
https://i.meee.com.tw/We0gwx2.jpeg
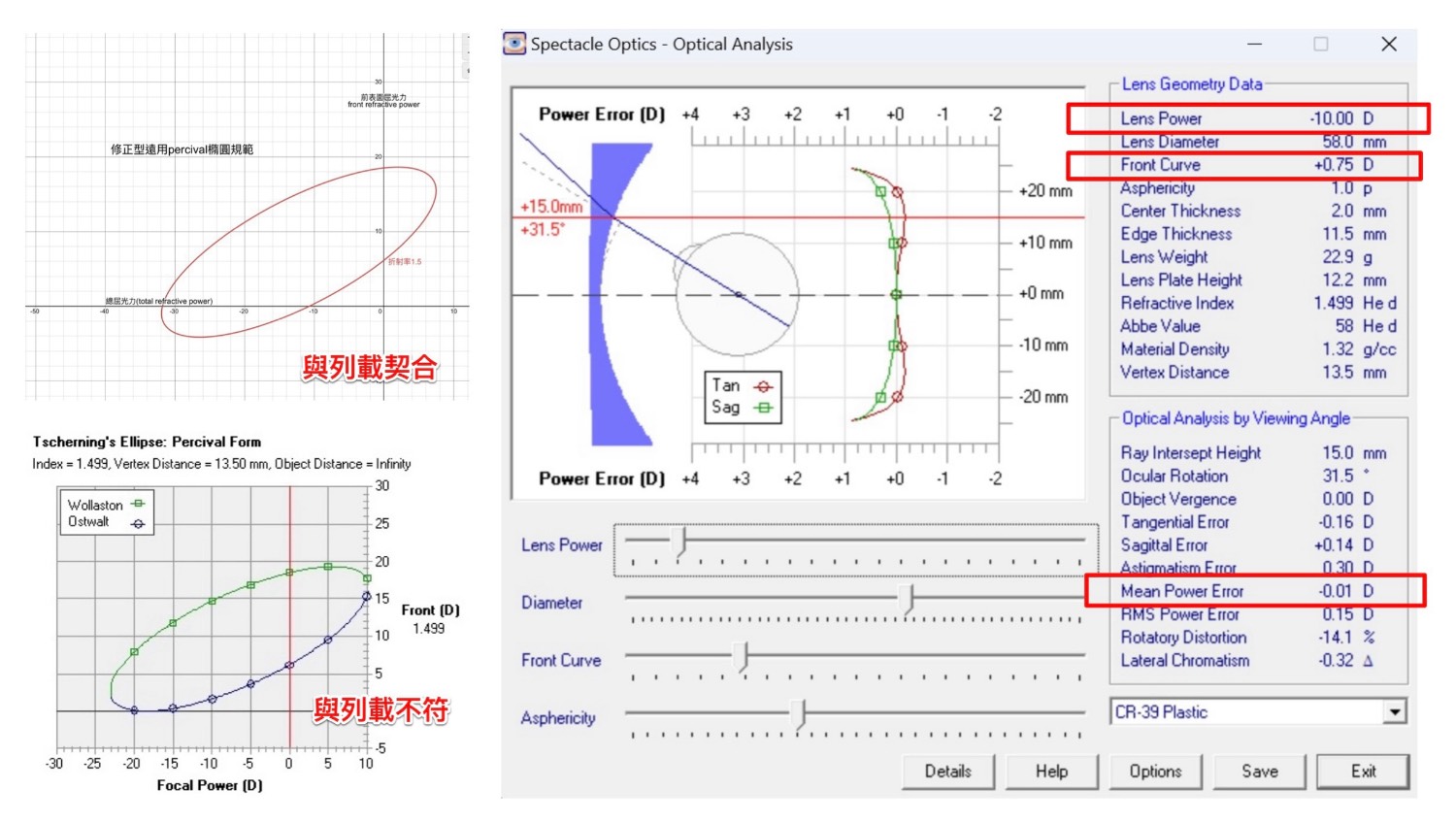
這顯示帕西瓦當時的數學計算存在邏輯推演錯誤,
我們猜測出他生前推算過程中可能出現紕漏的部分,
並成功重現吻合原始帕西瓦橢圓樣貌的函數形式。
https://i.meee.com.tw/f1FQ5ua.jpeg
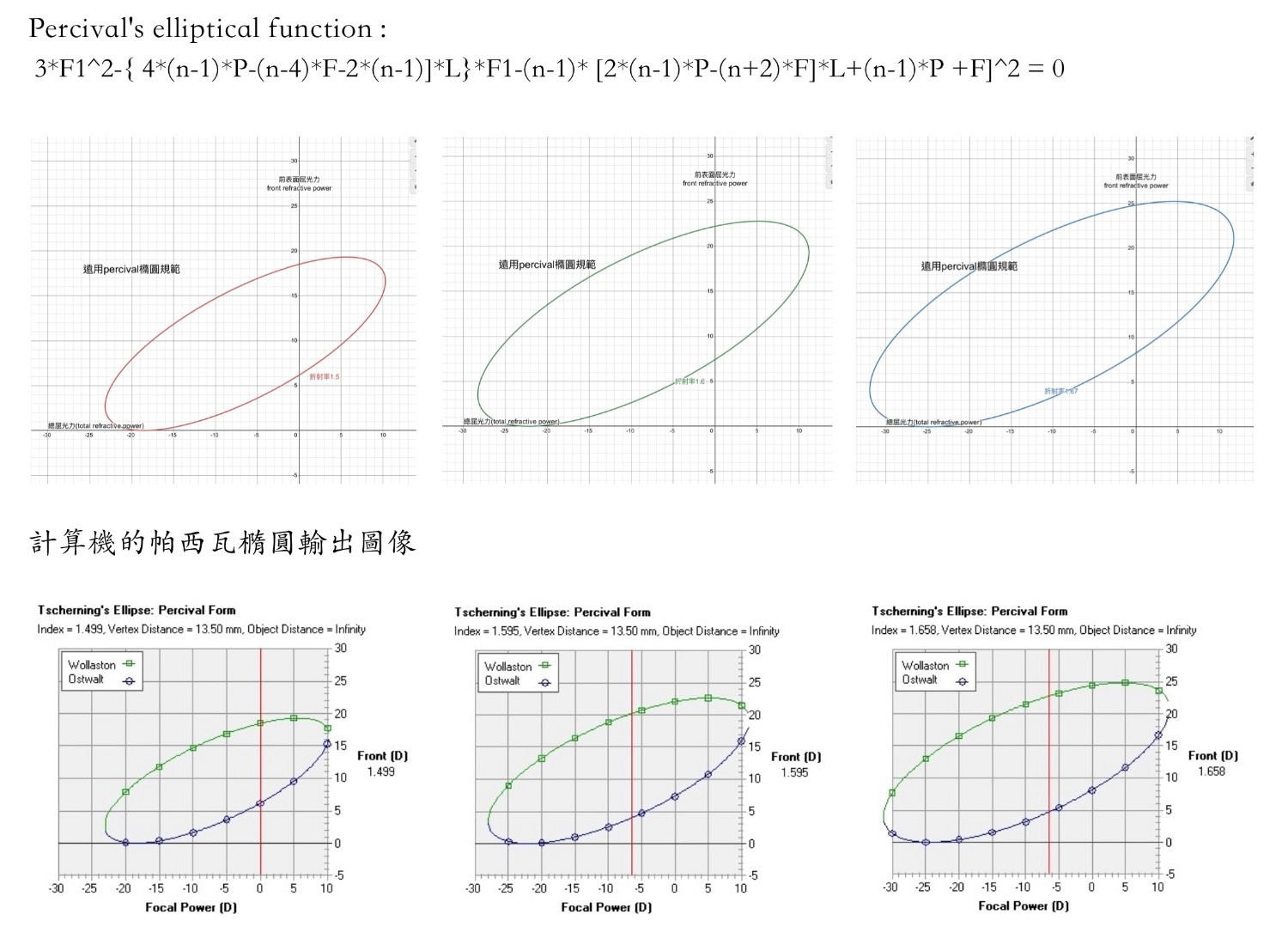
----------------------------------------------------
從方程式出發,依循數學的演繹,才能確保每一步皆清晰可溯,
這正是區辨真正理解與單純仿效的根本所在。
倘若知識僅停留於表層的敘述,它終將流於空泛而喪失深度與厚度。
唯有在自洽嚴整的數學架構中,方能為未來的探索奠下堅實的基礎。
語言或許可以模仿,但邏輯無法偽造,
而這也正是我們評判一切學術探索價值的黃金準則。
--
"The science I see delivers to me a feeling of great beauty,
but few others see it. This makes me sad."
—Feyman's Letters: The Beat of a Different Drum, October 1967
--
※ 發信站: 批踢踢實業坊(ptt.cc), 來自: 111.249.177.157 (臺灣)
※ 文章網址: https://www.ptt.cc/bbs/optical/M.1756313955.A.DB4.html
※ 編輯: kramnik (111.249.177.157 臺灣), 08/28/2025 10:19:17
討論串 (同標題文章)
完整討論串 (本文為第 2 之 2 篇):
0
1
optical 近期熱門文章
PTT消費區 即時熱門文章



